CFD Codes in Python
In my 6th semster, I have taken up the elective course under Dr. Yogesh G Bhumkar, Associate Professor, School of Mechanical Sciences. I was introduced to Python for developing inhouse codes to the problems. Python plays a pivotal role in Computational Fluid Dynamics (CFD), offering versatile libraries like OpenFOAM, PyTorch, and NumPy. It enables efficient simulation, data manipulation, and visualization, accelerating CFD research and analysis. Python's simplicity and extensibility make it an essential tool for engineers and researchers in the field. Prior to this I was used in doing simulations in ANSYS, where I used commercial CFD codes to solve the problems. Some of the problems I have worked on, are Dirichlet Problem, Neumann Problem, Poisson Equation, and solving Laplacian Heat Equation in different scenarios. The setup for the first three problem scenarios is as follows:
A 2 dimensional square plate is considered as the grid for our understanding. Temperature applied on the ends, change according to the boundary conditions set by us.
Classification of PDEs
The Laplace equation is a second-order partial differential equation that appears in various physical and mathematical contexts.
The laplace equation is given by: ∇2u=0. Where u is a scalar function of multiple variables
and ∇2 represents the Laplacian operator, which is the divergence of the gradient of u.
It can be classified into three types based on the nature of the solutions: elliptic, parabolic, and hyperbolic. 1. Elliptic PDE
The elliptic type of the Laplace equation typically describes steady-state or equilibrium problems where the solution does not
change with time. One example is the 2D steady-state heat distribution in a rectangular plate. We will solve this elliptic PDE in three
different scenarios: Dirichlet Boundary Condition, Neumann Boundary Condition and Dirichlet Boundary Condition with Heat Source.
A. Dirichlet Problem
The Dirichlet boundary conditions specify the values of the function (or field) being studied at the boundaries of the plate. Here, the temperatures
of the 4 sides of the plate are fixed. The code is:
import numpy as np
import matplotlib.pyplot as plt
l = 10.0
b = 10.0
N = 41
dx = l / (N - 1)
dy = b / (N - 1)
x = np.zeros((N, N))
y = np.zeros((N, N))
for i in range(N):
for j in range(N):
x[i, j] = dx * j
y[i, j] = dy * i
T = np.ones((N, N))
T[0, :] = 100
T[:, 0] = 50
T[N - 1, :] = 75
T[:, N - 1] = 50
A = 2 / (dx ** 2) + 2 / (dy ** 2)
for ct in range(1000):
for j in range(1, N - 1):
for i in range(1, N - 1):
T[i, j] = (((T[i + 1, j] + T[i - 1, j]) / (dx ** 2))+ ((T[i, j + 1] + T[i, j - 1]) / (dy ** 2))) / A
plt.contourf(x, y, T, levels=20, cmap='rainbow')
plt.colorbar(label='Temperature')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Temperature Contour')
plt.show()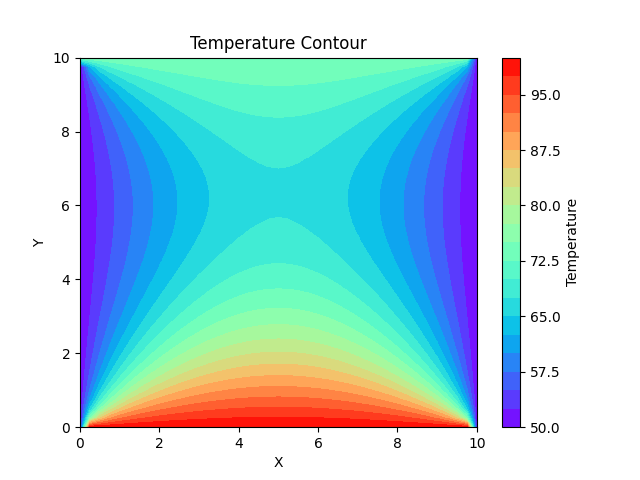
B. Neumann Boundary Condition
The Neumann boundary conditions specify the derivative of a function (or field) at the boundary of a domain, rather than the function's
actual value. These conditions are often used to model scenarios where there is a flux, flow, or gradient specified at the boundary.
Here, the upper and lower sides of the plate are adiabatic walls. Thereby, making the derivative of the temperature as zero.
The other two sides have temperature difference for us to observe the contours.
The code is:
import numpy as np
import matplotlib.pyplot as plt
l = 10.0
b = 10.0
N = 11
dx = l / (N - 1)
dy = b / (N - 1)
# Discretization of domain
x = np.zeros((N, N))
y = np.zeros((N, N))
for i in range(N):
for j in range(N):
x[i, j] = dx * (j)
y[i, j] = dy * (i)
# Boundary condition
T = np.ones((N, N))
T[:, 0] = 100
T[:, -1] = 50
# Iterative solving of PDE
for ct in range(10000):
for j in range(1, N - 1):
for i in range(1, N - 1):
T[i, j] = (T[i + 1, j] + T[i - 1, j] + T[i, j + 1] + T[i, j - 1]) / 4
T[0, 1:N - 1] = T[1, 1:N - 1]
T[N - 1, 1:N - 1] = T[N - 2, 1:N - 1]
# Plot the contour
plt.contourf(x, y, T, cmap='hot')
plt.colorbar(label='Temperature')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Temperature Contour')
plt.show()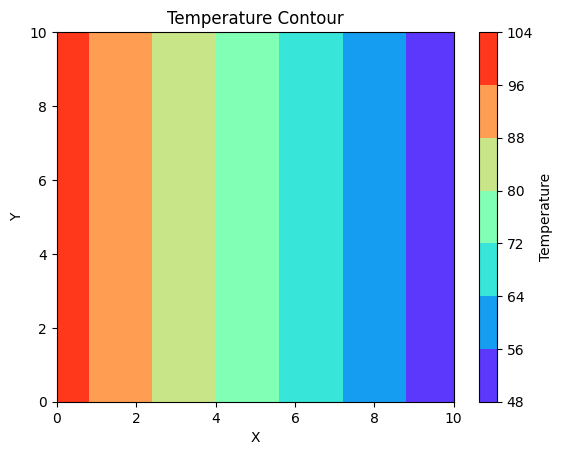
C. Poisson Equation
The Poisson equation in the presence of a heat source and Dirichlet boundary conditions, essentially describing a scenario
where there is a heat generation within a domain and the temperature is specified at the boundaries. Here, Heat generation is considered
to be coming from the middle of the plate and the dirichlet boundary condition applied on all four sides by keeping the temperature at 25°.
The contours can be observed and the effect of heat source can be seen here.
The code is:
import numpy as np
import matplotlib.pyplot as plt
l = 10.0
b = 10.0
N = 41
dx = l / (N - 1)
dy = b / (N - 1)
# Discretization of domain
x = np.zeros((N, N))
y = np.zeros((N, N))
for i in range(N):
for j in range(N):
x[i, j] = dx * (j)
y[i, j] = dy * (i)
# Boundary condition
T = np.ones((N, N))
# Iterative solution of PDE
A = (2 / (dx**2)) + (2 / (dy**2))
for ct in range(10000):
for j in range(1, N - 1):
for i in range(1, N - 1):
T[i, j] = (((T[i + 1, j] + T[i - 1, j]) / (dx**2)) + ((T[i, j + 1] + T[i, j - 1]) / (dy**2))) / A + \ (100 / A) * np.exp(-8 * ((x[i, j] - 5)**2 + (y[i, j] - 5)**2))
# Plot the contour
plt.contourf(x, y, T, cmap='rainbow')
plt.colorbar()
plt.xlabel('x')
plt.ylabel('y')
plt.title('Temperature Distribution')
plt.show()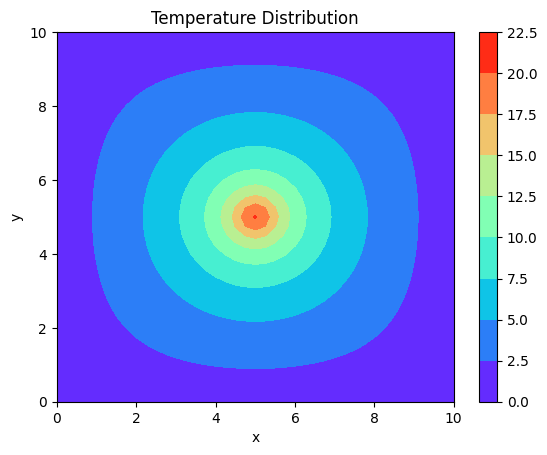
2. Parabolic PDE
The parabolic type of the Laplace equation describes problems that involve diffusion-like processes where the solution evolves over time.
An example is the 1D heat conduction equation: =α∇2 u. Here, represents the rate of change of temperature with respect to time, α is the thermal diffusivity, and ∇²u represents the Laplacian of temperature. This equation models the time-dependent heat conduction in a rod. The initial conditions are the temperature being 25°. The other details can be found in the code:
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(1, 101) # Domain definition
T = np.zeros((1000, 100)) # Initialization as an array
# Initializing the first time step using the given formula
T[0, :] = 75 * np.exp(-0.009 * ((x - 50) ** 2)) + 25
# Defining Timestep (dt), Cell size(dx), PDE parameter (alpha)
a = 0.1
dt = 1
dx = 1
# Solving Parabolic PDE
for t in range(1, 1000):
for i in range(1, 99):
T[t, 0] = 25
T[t, 99] = 25
T[t, i] = T[t - 1, i] + (a * dx / (dt ** 2)) * (T[t - 1, i + 1] - 2 * T[t - 1, i] + T[t - 1, i - 1])
# Visualizing over every 100 timesteps
for k in range(0, 1000, 100):
time_in_seconds = k * dt
plt.plot(x, T[k, :], label=f'Time: {time_in_seconds:.0f} s')
plt.xlabel('x')
plt.ylabel('Temperature (T)')
plt.title('Temperature Evolution over Time')
plt.legend() # Place the legend in the upper right corner
plt.show()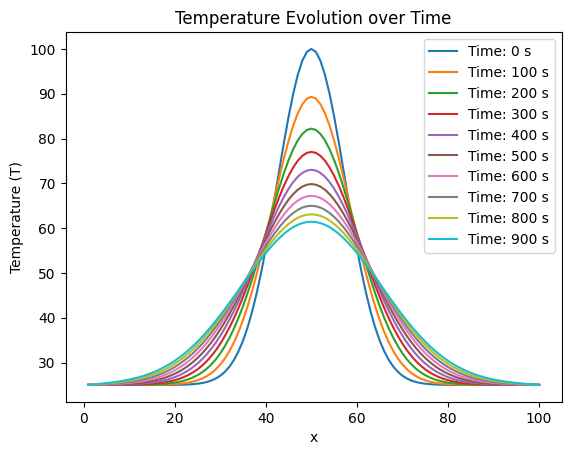
3. Hyperbolic PDE
The hyperbolic type of the Laplace equation is associated with wave-like phenomena where disturbances propagate through space and
time. An example is the 1D wave equation: = c²∇²u.
Here, represents the acceleration of the wave-like disturbance, c is the wave speed, and
∇²u represents the Laplacian of the disturbance. This equation models various wave phenomena, such as vibrations in a string,
sound waves, and electromagnetic waves. The initial condition of this case here is a sinusoidal function. The other details can be found in the code:
import numpy as np
import matplotlib.pyplot as plt
x = np.arange(1, 101) # Domain definition
y = np.concatenate((np.zeros(30), np.arange(0, np.pi + np.pi / 31, np.pi / 31), np.zeros(38)))
u = np.zeros((10, 100)) # Initialization as an array
# Initializing the first time step using sine of y
u[0, :] = np.sin(y)
a = 0.1
dt = 1
dx = 1
c = -1
for t in range(1, 10):
for i in range(1, 99):
u[t, i] = u[t - 1, i] - 0.5 * ((c * dt) / dx) * (u[t - 1, i + 1] - u[t - 1, i - 1])
# Visualizing over each time step
for k in range(10):
time_step = k + 1
plt.plot(x, u[k, :], label=f'Time Step {time_step}', linestyle='-', linewidth=1)
plt.title('Hyperbolic Wave Equation', fontweight='bold')
plt.xlabel('1D Spatial Domain', fontweight='bold')
plt.ylabel('Amplitude', fontweight='bold')
plt.show()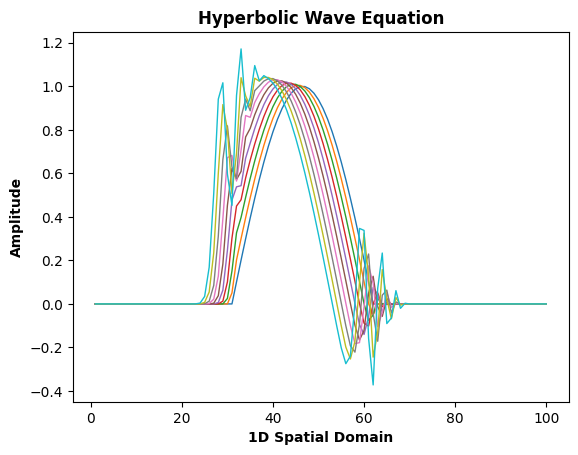
4. Streamlines through a chamber
Here, we examine the behavior of a two-dimensional, inviscid, and incompressible fluid that flows steadily through a confined chamber
positioned between an inlet and an outlet. This fluid flow is characterized by an absence of vorticity owing to its irrotational nature,
resulting in a vorticity value of zero. Consequently, the governing dynamics of the fluid are encapsulated by an Elliptic Partial
Differential Equation, which defines its stream function as follows:
+=0.
We approach this context with two distinct scenarios; Single Inlet Single Outlet configuration and Single Inlet Multiple Outlets configuration. In the first case, our consideration is directed towards openings strategically situated diagonally opposite to each other, maintaining a mutually facing alignment. This particular arrangement is mirrored by the observable pattern of streamlines. The code is as follows:
import numpy as np
import matplotlib.pyplot as plt
l = 10.0
b = 10.0
N = 41
dx = l / (N - 1)
dy = b / (N - 1)
# Discretisation of domain
x = np.zeros((N, N))
y = np.zeros((N, N))
for i in range(N):
for j in range(N):
x[i, j] = dx * j
y[i, j] = dy * i
# Boundary condition
p = np.ones((N, N))
p[:, 0] = 2
p[N - 1, 0:33] = 2
p[0, 8:N] = 4
p[:, N - 1] = 4
p[0, 0:9] = np.arange(2, 4.25, 0.25)
p[N - 1, 32:N] = np.arange(2, 4.25, 0.25)
A = 2 / dx ** 2 + 2 / dy ** 2
# Solution of PDE
for ct in range(10000):
for i in range(1, N - 1):
for j in range(1, N - 1):
p[i, j] = ((p[i + 1, j] + p[i - 1, j]) / dx ** 2 + (p[i, j + 1] + p[i, j - 1]) / dy ** 2) / A
# Plotting rainbow-filled contours and contour lines
plt.contourf(x, y, np.rot90(p, 2), 50, cmap='rainbow')
contour_lines = plt.contour(x, y, np.rot90(p, 2), 15, colors='black')
plt.clabel(contour_lines, inline=True, fontsize=8)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Rainbow-Filled Contours with Contour Lines')
plt.colorbar(label='Value')
plt.show()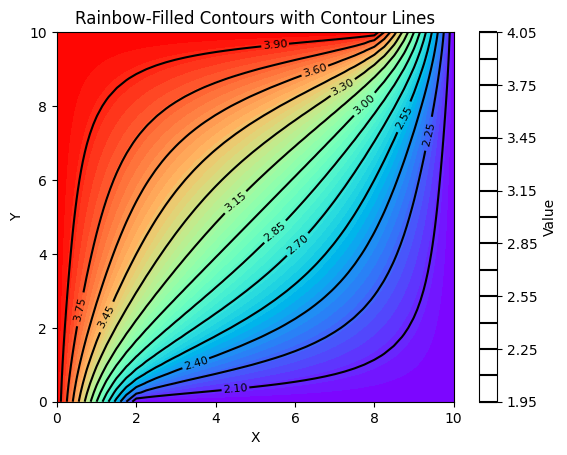
import numpy as np
import matplotlib.pyplot as plt
l = 10.0
b = 10.0
N = 41
dx = l / (N - 1)
dy = b / (N - 1)
# Discretisation of domain
x = np.zeros((N, N))
y = np.zeros((N, N))
for i in range(N):
for j in range(N):
x[i, j] = dx * j
y[i, j] = dy * i
# Boundary condition
p = np.ones((N, N))
p[:, 0] = 2
p[40, 0:7] = 2
p[40,7:12] = np.arange(2 + 1/6, 2 + 5/6, 1/6)
p[40,11:18] = 8/3
p[40,18:23] = np.arange(8/3 + 1/6, 8/3 + 5/6, 1/6)
p[40,22:29] = 10/3
p[40,29:34] = np.arange(10/3 + 1/6, 10/3 + 5/6, 1/6)
p[40,33:40] = 4
p[0, 0:8] = np.arange(2, 3.75 + 0.25, 0.25)
p[0, 8:40] = 4
p[:, 40] = 4
A = 2 / dx ** 2 + 2 / dy ** 2
# Solution of PDE
for ct in range(10000):
for i in range(1, N - 1):
for j in range(1, N - 1):
p[i, j] = ((p[i + 1, j] + p[i - 1, j]) / dx ** 2 + (p[i, j + 1] + p[i, j - 1]) / dy ** 2) / A
# Streamline visualization using contours
plt.contourf(x, y, np.rot90(p, 2), 50, cmap='rainbow')
contour_lines = plt.contour(x, y, np.rot90(p, 2), 30, colors='black')
plt.clabel(contour_lines, inline=True, fontsize=8)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Rainbow-Filled Contours with Contour Lines')
plt.colorbar(label='Value')
plt.show()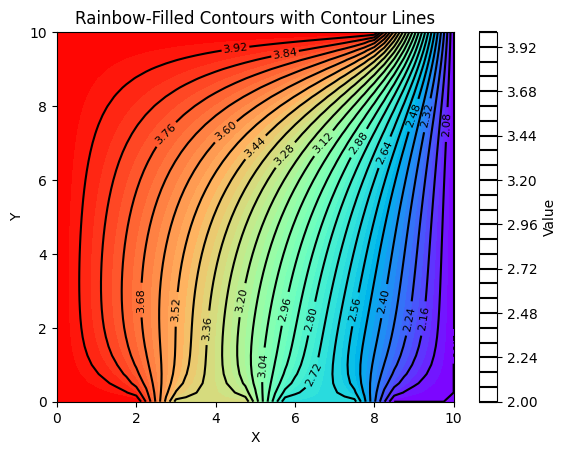
I would like to thank Dr. Yogesh G Bhumkar for his guidance and constant encouragement towards taking up the challenge to develop the codes instead of using the available commercial codes. His interactive classroom approach has inspired me to venture into this new field. I would like to take this opportunity to thank my batchmate, Mr. Bharath Ram for helping me out in clutch situations.
